Content Domain II: Patterns, Algebra, and Functions

Which of the following equations represents the inverse of y = ^{6x − 4}/_{1 + 3x}y equals the quantity 6x minus 4 over the quantity 1 plus 3x?

1. y = ^{x − 4}/_{3x + 6}y equals the quantity x minus 4 over the quantity 3x plus 6
2. y = ^{x + 4}/_{6 − 3x}y equals the quantity x pluss 4 over the quantity 6 minus 3x
3. y = ^{1 + 3x}/_{6x − 4}y equals the quantity 1 plus 3x over the quantity 6x minus 4
4. y = ^{1 − 3x}/_{6x + 4}y equals the quantity 1 minus 3xover the quantity 6x plus 4

Correct Response and Explanation (Show Correct ResponseHide Correct Response)

B. This question requires the examinee to perform operations with functions, including compositions and inverses. To find the inverse of a function of the form y = f(x)y = f of x, the original equation is rearranged by solving it for x as a function of y: y = ^{6x − 4}/_{1 + 3x} ⇒ y(1 + 3x) = 6x − 4 ⇒ y + 3xy = 6x − 4 ⇒ y + 4 = 6x − 3xy ⇒ y + 4 = x(6 − 3y) ⇒ x = ^{y + 4}/_{6 − 3y}y equals the quantity 6x minus 4 over the quantity 1 plus 3x which becomes y left parenthesis 1 plus 3x right parenthesis equals 6x minus 4 which becomes y plus 3xy equals 6x minus 4 which becomes y plus 4 equals 6x minus 3xy which becomes y plus 4 equals x left parenthesis 6 minus 3y right parenthesis which becomes x equals y plus 4 over the quantity 6 minus 3y. Exchanging the variables x and y results in the inverse function f^–1, y = ^{x + 4}/_{6 − 3x}f superscript negative 1, y equals the quantity x + 4 over the quantity 6 minus 3x

Given the table of orders and total costs above, and that there is a solution to the problem, which of the following matrix equations could be used to find d, p, and g, the individual prices for a soft drink, a large pizza, and garlic bread respectively?

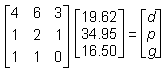
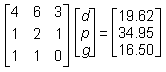
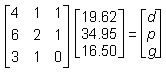
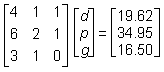
Correct Response and Explanation (Show Correct ResponseHide Correct Response)

D. This question requires the examinee to solve systems of linear equations or inequalities using a variety of methods. The system of linear equations can be solved using matrices. Each order can be expressed as an equation, with all three equations written with the variables in the same sequence. The first order is represented by the equation 4d + p + g = 19.624d plus p plus g equals 19.62, the second order by 6d + 2p + g = 34.956d plus 2p plus g equals 34.95, and the third order by 3d + p = 16.503d plus p equals 16.50. The rows of the left-hand matrix contain the coefficients of d, p, and g for each equation: (4 1 1), (6 2 1), and (3 1 0)left parenthesis 4 1 1 right parenthesis, left parenthesis 6 2 1 right parenthesis, and left parenthesis 3 1 0 right parenthesis. The middle matrix contains the variables, d, p, g. The right-hand matrix vertically arranges the constants of the equations.

Which of the following is equivalent to the equation 3 log₁₀ x − 2 log₁₀ y = 173 log subscript 10 x minus 2 log subscript 10 y equals 17?

1. 3x − 2y = 10¹⁷3x minus 2y equals 10 to the power of 17
2. x³ − y² = 10¹⁷x cubed minus y squared equals 10 to the power of 17
3. ^x3/_y² = 10¹⁷x cubed over y squared equals 10 to the power of 17
4. ^3x/_2y = 10¹⁷3x over 2y equals 10 to the power of 17

Correct Response and Explanation (Show Correct ResponseHide Correct Response)

C. This question requires the examinee to apply the laws of exponents and logarithms.
Nlog_a M = log_a M^N ⇒ 3log₁₀ x = log₁₀ x³ and 2log₁₀ y = log₁₀ y²Nlog subscript a M equals log subscript a M superscript N which becomes 3log subscript 10 x equals log subscript 10 x cubed and 2log subscript 10 y equals log subscript 10 y squared.
Log_a M − log_a N ⇒ log_a ^M/_N ⇒ log₁₀ x³ − log₁₀ y² = log₁₀ ^x3/_y²Log subscript a M minus log subscript a N which becomes log subscript a M over N which becomes log subscript 10 x cubed minus log subscript 10 y squared equals log subscript 10 x cubed over y squared.
Since log_a M = N is equivalent to a^N = M, then log₁₀ ^x3/_y² = 17 is equivalent to 10¹⁷ = ^x3/_y²log subscript a M equals N is equivalent to a superscript N equals M, then log subscript 10 x cubed over y squared equals 17 is equivalent to 10 to the power of 17 equals x cubed over y squared.

Which of the following represents the domain of the function f(x) = The square root of the quantity 2x plus 3 over 3x plus 1?

Correct Response and Explanation (Show Correct ResponseHide Correct Response)

B. This question requires the examinee to analyze rational, radical, absolute value, and piece-wise defined functions in terms of domain, range, and asymptotes. Unless otherwise specified, the domain of a function is the range of values for which the function has a real number value. A rational function must have a nonzero denominator, and solving the equation 3x + 1 = 0 yields x = – ¹/₃3x plus 1 equals 0 yields x equals negative 1 third. Thus this value must be excluded from the domain. The radical expression in the numerator must have a non-negative argument and solving the inequality 2x + 3 ≥ 0 yields x ≥ –³/₂2x plus 3 is greater than or equal to 0 yields x is greater than or equal to negative 3 over 2. Putting these two results together results in –³/₂ ≤ x < –¹/₃ or x > –¹/₃negative 3 over 2 is less than or equal to x is less than negative 1 third or x is greater than negative 1 third. The "or" represents the union of the two sets defined by the inequalities, or the union of the two intervals.